För många DC-DC-omvandlare finns ett "ganska" resonans lågpassfilter involverat vid utgången och det ändrar sin fasvinkel "ganska" snabbt från 0 grader till 180 grader över en kort del av spektrumet. Här är den allmänna idén att använda L = 100 uH och C = 100 uF med en effektiv induktorseriemotstånd på 0,3 ohm: -

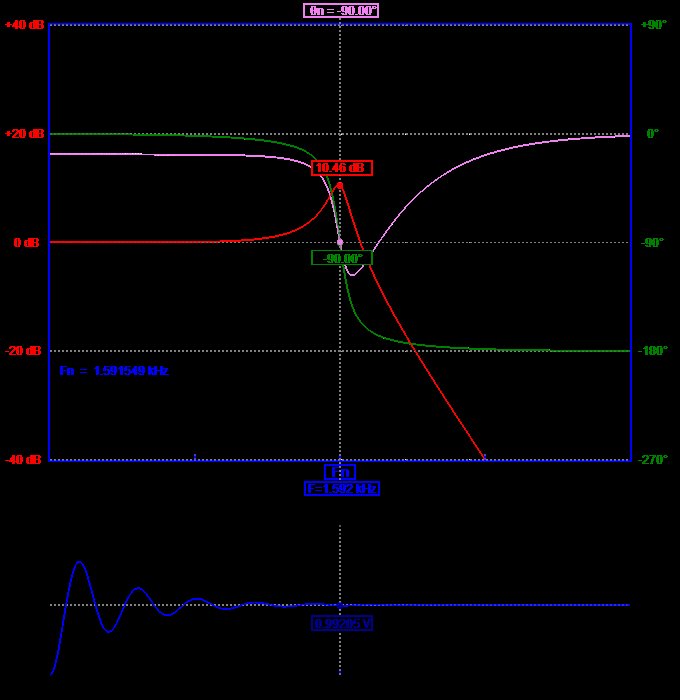
Kalkylatorkälla.

Så inom detta område är det möjligt att uppleva instabilitet (på grund av feedback-systemet som försöker hålla Vout på en konstant nivå). Fasvinkeln ändras 180 grader så att den kan konvertera negativ återkoppling till en positiv positiv återkoppling. Lösningen är att applicera en fasledarkrets "inuti slingan" som förhindrar att fasvinkeln når nära 180 grader medan amplituden fortfarande är större än enhet.

Detta lyfter baslinjefasvinkeln (närmar sig vid högre frekvenser) till något mycket mindre (och mer stabil) än 180 grader. Observera att kiselförstärkaren som används i återkopplingsslingan faller till enhetsförstärkning vanligtvis många gånger högre än filterens korsningspunkt. Denna enhetsfördelningspunkt är där förstärkningsmarginalen definieras och därför bör den till stor del inte vara relaterad till övergångspunkten för LC-nätverket.

Så omedelbart handlar det föredragna "samtalet" om fasmarginal och att motverka vad LC-kretsen gör mot fasvinkeln. Belastningen på utgången kan vara ganska lätt och detta kommer att höja resonans toppens höjd och därmed kommer den punkt vid vilken förstärkningen passerar genom enhet att flyttas till en högre frekvens men för förändringen i fasvinkeln kommer detta att inträffa nära Fn och det är den här delen av spektrumet som ger störst huvudvärk till en designer.

Med andra ord vet vi vad det värsta fallet är - fasen förändras snabbt, vi pratar om att använda en faskompensator för att förhindra att fasvinkeln blir 180 grader.

Denna typ av applikation lämpar sig för att diskutera fasmarginal snarare än vinstmarginal.

I allmänhet, även om det finns undantag, förbehåll och subtiliteter, berättar fasmarginalen dig mer om hur systemets svar kommer att se ut. Till exempel hur mycket överskott och ringning du kan förvänta dig på grund av belastningstransienter. Det kan också berätta om det finns mer prestanda genom att öka bandbredden (eftersom fasmarginalen är hög).

Vanligtvis använder många designers 45 grader som den absolut minsta acceptabla fasmarginalen över komponenttoleranser etc. och 60 som ett typiskt mål.

Förstärkningsmarginal är också viktigt, men det ger inte så mycket information om systemets svar. Det berättar hur mycket variation i systemförstärkning du kan tåla innan systemet blir instabilt. Ett typiskt mål kan vara 12 dB.

En typisk designmetod är att använda en modell för att utforma kompensationen inriktad på en viss fasmarginal. Simulera sedan kanske med hjälp av Monte-Carlo-tekniker, kontrollera att du uppfyller din minsta fasmarginal och en rimlig vinstmarginal. Om endera är avstängd, upprepa designen. Slutligen mäta svaret i labbet för att vara säker på att det korrelerar.

Generellt sett är fasmarginalen viktigare (mer kritisk) än förstärkningsmarginalen för alla system med feedback. Förklaringen är relativt enkel: Fasmarginalen (resp. Förstärkningsmarginal) ger dig den ytterligare (oönskade) fasförskjutningen (resp. Ytterligare förstärkning) som kommer att föra den slutna slingan till området med instabilitet.

Och sannolikheten att någonstans inom återkopplingsslingan en ytterligare (dold) fasförskjutning skulle inträffa (t.ex. på grund av okända kapacitiva effekter) är mycket större än risken för oönskad förstärkning.Fasmarginalen är därför en mycket mer kritisk stabilitetsindikator än förstärkningsmarginalen.