Nej, det är inte korrekt, om bara för att varken lysdioden eller strömförsörjningen är 3,3 V. Strömförsörjningen kan vara 3,28V och LED-spänningen 3,32V, och då håller den enkla beräkningen för seriemotståndet inte längre.

Modellen för en LED är inte bara ett konstant spänningsfall, utan snarare en konstant spänning i serie med ett motstånd, det interna motståndet. Eftersom jag inte har data för din LED, låt oss titta på denna egenskap för en annan LED, Kingbright KP-2012EC LED:

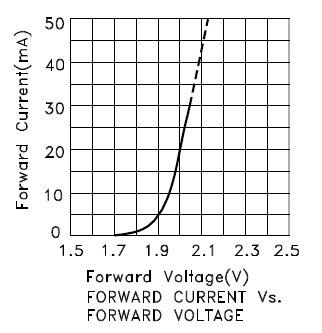
För strömmar högre än 10mA är kurvan rak och lutningen är det motsatta mot det inre motståndet. Vid 20mA är framspänningen 2V, vid 10mA är detta 1,95V. Då är det interna motståndet

\ $ R_ {INT} = \ dfrac {V_1 - V_2} {I_1 - I_2} = \ dfrac {2V - 1.95V} {20mA - 10mA} = 5 \ Omega \ $.

Den inneboende spänningen är

\ $ V_ {INT} = V_1 - I_1 \ gånger R_ {INT} = 2V - 20mA \ times 5 \ Omega = 1.9V. \ $

Antag att vi har en strömförsörjning på 2V, då ser problemet lite ut som originalet, där vi hade 3,3V för både strömförsörjning och LED. Om vi ​​skulle ansluta lysdioden genom ett 0 \ $ \ Omega \ $ motstånd (båda spänningarna är trots allt lika!) Får vi en LED-ström på 20 mA. Om strömförsörjningsspänningen skulle ändras till 2,05V, bara en 50mV ökning, skulle LED-strömmen vara

\ $ I_ {LED} = \ dfrac {2.05V - 1.9V} {5 \ Omega} = 30mA. \ $

Så en liten spänningsförändring kommer att resultera i en stor strömförändring. Detta visas i grafens branthet och det låga inre motståndet. Det är därför du behöver ett externt motstånd som är mycket högre, så att vi har strömmen bättre under kontroll. Naturligtvis ger ett spänningsfall på 10mV över, säg 100 \ $ \ Omega \ $ bara 100 \ $ \ mu \ $ A, vilket knappast kommer att synas. Därför krävs också en högre spänningsskillnad.

Du behöver alltid ett tillräckligt stort spänningsfall över motståndet för att ha en mer eller mindre konstant LED-ström.

Du behöver alltid en strömbegränsande enhet. När du använder en spänningskälla bör du alltid ha ett motstånd, tänk på vad som händer när spänningen ändras med en liten mängd. Med inget motstånd skulle LED-strömmen skjuta upp (tills du når en termisk baserad gräns på grund av LED-materialen). Om du hade en strömkälla, skulle du inte behöva ett seriemotstånd eftersom lysdioden skulle gå på aktuell källnivå.

Det är också osannolikt att lysdioden framåt alltid är exakt densamma som utbudet. Det kommer att finnas ett intervall som nämns i databladet. Så även om din leverans exakt matchade den typiska framspänningen, skulle olika lysdioder köra med mycket olika strömmar och därmed ljusstyrka.

I-V-förhållandet i en diod är exponentiellt, så att applicera en spänningsskillnad på 3,3 V +/- 5% på en LED med ett nominellt 3,3 V-fall kommer inte att resultera i 5% variation i intensitet.

Om spänningen är för låg kan lysdioden vara svag; om spänningen är för hög kan lysdioden skadas. Som Hans säger räcker antagligen inte en 3,3 V-matning för en 3,3 V LED.

När du kör en LED är det bättre att ställa in strömmen, inte spänningen, eftersom strömmen har en mer linjär korrelation med ljusintensiteten. Att använda ett seriemotstånd är en bra approximation av att ställa in strömmen genom lysdioden.

Om du inte kan använda en strömförsörjning med tillräckligt med utrymme för att tillåta ett strömställande motstånd kan du kanske använda en aktuell spegel. Det kräver fortfarande något spänningsfall, men kanske inte så mycket som du behöver för ett motstånd.

Du behöver ett spänningsfall över strömbegränsningsmotståndet för att det ska fungera. Och det spänningsfallet borde vara stort för att undvika höga strömmar när din 3.3V är lite avstängd (kanske 3,45V en stund). Om du skulle köra en LED med 1V spänningsfall över ett motstånd och matningen är 1V högre, skulle du ha ca. den dubbla strömmen.

En lysdiod behöver en konstant ström för att lysa. En konstant strömkälla behöver dock förmodligen mer än 3,3 V för en blå LED, såvida du inte använder en buck-boost-version.

Om strömkällan var exakt 3,3V och spänningsfallet över lysdioden var 3,3V skulle du inte behöva ett strömbegränsande motstånd. Världen är dock inte perfekt och det finns brister i allt!

Du kan bara beräkna ett lämpligt säkerhetsmotståndsvärde efter att du har redovisat strömförsörjningskonfigurationen och variationen i LED-framspänningen. Om du tror att \ $ V_ {SOURCE} -V_ {LED} \ $ kan ha ett fel / variation upp till \ $ 0.5 \ mbox {} V \ $, beräknar du motståndsvärdet för det. Som exempel är fallet \ $ \ pm 0.5 \ mbox {} V \ $, vilket inte är orimligt för en 10% 5V-källa:

$$ \ frac {V} {I} = \ frac {0.5 \ mbox {} V} {20 \ mbox {mA}} = 25 \ mbox {} \ Omega $$

Observera att detta förmodligen inte är en bra idé i praktiken, men det är möjligt.

Om framspänningen och matningsspänningen är nästan lika, kommer användning av ett motstånd att ge resultat som är mycket känsliga för variationer i matningsspänning eller LED-egenskaper. Om motståndet är dimensionerat för att undvika att skada lysdioden om det visar sig att matningsspänningen är högst och LED: s inneboende spänning är minimal, lyser lysdioden bara med en bråkdel av dess möjliga ljusstyrka om matningsspänningen är som minimum LED-intrunsisk spänning är maximalt.

Att använda någon typ av strömreglerande krets ger mycket bättre resultat, även om de flesta enkla strömreglerande kretsar har en viss mängd överensstämmelsesspänning. Förmodligen det enklaste att göra i många fall är att använda ett LED-drivrutinschip med en inbyggd boosterkrets. Vissa av dem kan göra ett bra jobb med att reglera LED-ljusstyrka oberoende av matningsspänning.

Även om spänningarna var desamma måste du fortfarande lägga till ett motstånd. Den enda gången du inte lägger till ett motstånd är när strömutgången från källan är mindre än eller lika med den mängd som behövs, till exempel anslutning av en vit lysdiod till en CR2023. Inget motstånd behövs, eftersom batteriets interna motstånd begränsar strömmen till en acceptabel nivå.

Oroa dig inte för att lägga till ett motstånd eftersom det är det billigaste du kan lägga till för att skydda din LED, om du inte är hanterar LED med hög ström.

Jag hände med detta av misstag, och det finns ingenting som att lägga till kommentarer till en gammal eld ... Men ...

Om du kör lysdioden från en källa med mycket lågt internt motstånd än lysdioden är känslig för små förändringar i matningsspänningen. Om du kör LED-lampan från en stor strömförsörjning som kan leverera förstärkare och den driver 10 MV högre kan du laga LED-lampan. Observera att i många fall, till exempel billiga ficklampor, lysdioderna ses som engångsbruk och de är ganska säkra på att batteriets polspänning inte kommer att bli mer än vad som är normalt för den typen av batterikemi; Lysdioden fungerar antagligen över spec eller precis vid kanten med nya batterier. Beroende på enheternas framåtriktade ledningskurva kanske du kanske inte kan säga 20MA till en vit eller blå lysdiod på en 3,3 V-matning. Och om du gör matematik kommer det inte att ge dig mycket spännings latitud att sätta ett 5 ohm motstånd i serie med LED. Men fram till den här tiden har vi bara varit bekymrade över LED: ns hälsa, vilket verkar vara snällt. Jag skulle vara mycket mer orolig för att överbelasta en av I / O-stiften på en mikrokontroller som kostade mig några dollar än att laga en LED som kan fås för under 2 cent på eBay. Så, om jag skulle ansluta en lysdiod till utgången från ett dyrt chip med en 3,3 V Vcc, även om lysdioden var märkt till 3,3 VI skulle det antagligen lägga till några hundra ohm och köra bort lysdioden bara några få gånger än riskera att skada den dyra delen. Om jag ville att lysdioden skulle vara ljus skulle jag använda en transistor eller ett dedikerat chip för att driva den. Med det tillvägagångssättet kan du köra LED-lampan från den råa strömförsörjningen och använda ett större släppmotstånd. Det ger dig mer latitud med lysdioden och det finns mindre risk att skada den dyra delen genom att överbelasta utdata.

LEDS kan hantera mycket mer PEAK-ström än steady state. Studera LED-databladet och PWM sedan LED-lampan inom dess PEAK-arbetscykelgränser och du behöver då inte ett motstånd