Sinusformade vågor har inte övertoner eftersom det är exakt sinusvågor som tillsammans kan konstruera andra vågformer. Grundvågen är en sinus, så du behöver inte lägga till något för att göra den till sinusformad signal.

Om oscilloskopet. Många signaler har ett stort antal övertoner, vissa, som en fyrkantig våg, i teorin oändliga.

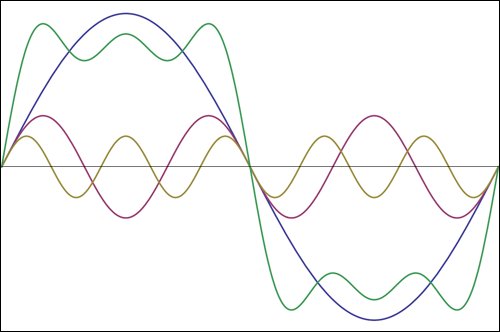
Detta är en partiell konstruktion av en fyrkantig våg. Den blå sinus som visar en period är grundläggande. Sedan finns det den tredje övertonen (fyrkantiga vågor har inte ens övertoner), den lila. Dess amplitud är 1/3 av grundläggande, och du kan se att den är tre gånger grundfrekvensen, eftersom den visar tre perioder. Samma för den femte övertonen (brun). Amplituden är 1/5 av grundläggande och den visar 5 perioder. Att lägga till dessa ger den gröna kurvan. Detta är ännu inte en bra fyrkantig våg, men du ser redan de branta kanterna, och den vågiga horisontella linjen kommer i slutändan att bli helt horisontell om vi lägger till fler övertoner. Så så kommer du att se en fyrkantig våg på omfånget om bara upp till den femte övertonen visas. Detta är verkligen det minsta, för en bättre rekonstruktion behöver du mer övertoner.

Liksom varje icke-sinusformad signal kommer den AM-modulerade signalen att skapa övertoner. Fourier visade att varje upprepande signal kan dekonstrueras till en grundläggande (samma frekvens som vågformen) och övertoner som har frekvenser som är multiplar av det grundläggande. Det gäller även för icke-upprepande vågformer. Så även om du inte lätt ser hur de skulle se ut, är analysen alltid möjlig.

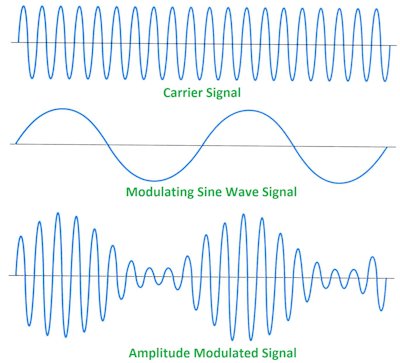
Detta är en grundläggande AM-signal, och den modulerade signalen är produkten från bäraren och basbandssignalen. Nu

\ $ sin (f_C) \ cdot sin (f_M) = \ dfrac {cos (f_C - f_M) - cos (f_C + f_M)} {2} \ $

Så att du kan se att även en produkt av sinus kan uttryckas som summan av sinus, det är båda cosinus (övertonerna kan ha sin fasförskjutning, i detta fall 90 °). ) \ $ och \ $ (f_C + f_M) \ $ är sidebanden till vänster och höger om bärfrekvensen \ $ f_C \ $.

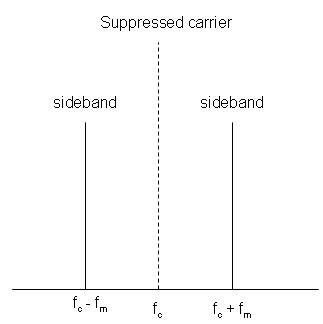
Även om din basbandssignal är en mer komplex signal kan du bryta isär den modulerade signalen i separata signaler.

Pentium100s svar är ganska fullständigt, men jag skulle vilja ge en mycket enklare (men mindre exakt) förklaring.

Anledningen till att senvågor har (helst) bara en överton är att sinus är "jämnaste" periodiska signal som du kan ha, och det är därför den "bästa" när det gäller kontinuitet, derivabilitet och så vidare. Av denna anledning är det bekvämt att uttrycka vågformer i termer av sinusvågor (du kan också göra det med andra vågor, såväl som de är \ $ C ^ {\ infty} \ $).

Bara ett exempel : varför i vattnet ser du vanligtvis böjda vågor? (för denna skull, ignorera effekten av stranden eller vinden) Återigen beror det på att det är formen som kräver mindre energi för att bildas, eftersom alla ramper och kanter är släta.

I vissa fall, som Hammondorgel används sinusvågor för att komponera signalen, för med sönderdelning är det möjligt att syntetisera många (nästan alla) ljud.

Där är en vacker animation av LucasVB som förklarar Fourier-sönderfallet av en fyrkantig våg:

Dessa bilder förklarar bättre kvadratvågsnedbrytning i övertoner:

Du kan sönderdela vilken vågform som helst i en oändlig serie av sinusvågor som läggs ihop. Detta kallas Fourier-analys (om den ursprungliga vågformen upprepas) eller Fourier-transformation (för vilken vågform som helst).

Om en upprepande vågform (som en fyrkantvåg), när du gör Fourier-analys, finner du att alla sines som komponerar vågformen har frekvenser som är en heltalsmultipel av frekvensen för den ursprungliga vågformen. Dessa kallas "övertoner".

En sinusvåg har bara en överton - den grundläggande (ja, den är redan sinus, så den består av en sinus). Fyrkantig våg kommer att ha en oändlig serie av udda övertoner (det vill säga för att göra en fyrkantvåg av sines måste du lägga till sines för varje udda multipel av grundfrekvensen).

Övertonerna genereras genom förvrängning sinusvåg (även om du kan generera dem separat).

Varför är det här viktigt:

1. Du kan skapa en sinusvåg av vilken våg som helst med en fast frekvens, så länge du har ett filter som passerar grundfrekvensen, men blockerar 2x frekvens (eftersom du bara skulle lämna en överton på plats).
2. Egentligen kan du skapa en sinusvåg som har en annan frekvens än originalet - använd bara ett bandpassfilter för att passera övertonen du vilja. Du kan använda detta för att få en sinusvåg med en frekvens som är en multipel av frekvensen för en annan sinus - bara snedvrida originalets sinus och plocka ut den överton som du vill ha.
3. RF-system måste lägga ut vågformer som inte innehåller övertoner utanför det tillåtna frekvensområdet. Så här kan en PWM-strömförsörjning (driftsfrekvens ~ 100kHz, fyrkantvåg) störa FM-radio (driftsfrekvenser 88-108MHz, 11-12MHz (IF)).
4. Om du vill ha en fyrkant våg med mycket snabba stigningstider / nedgångstider, måste bandbredden i ditt system vara mycket bredare än den grundläggande frekvensen för din fyrkantvåg.

Derivat - förändringshastighet - för en sinusoid är en annan sinusoid med samma frekvens, men fasförskjuten. Verkliga komponenter - ledningar, antenner, kondensatorer - kan följa förändringarna (av spänning, ström, fältstyrka etc.) på derivaten såväl som de kan följa originalsignalen. Ändringshastigheterna för signalen, signalens förändringshastighet, förändringshastigheten för signalens förändringshastighet etc. finns alla och är ändliga.

Övertonerna hos en fyrkantig våg existerar eftersom förändringshastigheten (första derivatet) av en fyrkantig våg består av mycket höga, plötsliga toppar; oändligt höga toppar, i gränsfallet med en så kallad perfekt fyrkantvåg. Verkliga fysiska system kan inte följa så höga priser, så signalerna blir förvrängda. Kapacitans och induktans begränsar helt enkelt deras förmåga att svara snabbt, så de ringer. ) vid långsammare hastigheter, så att en krets inte svarar i den takt som den träffas av spikarna som är kanterna på fyrkantvågen. Det ringer eller svänger också när energin försvinner.

Ett konceptuellt block kan komma från att begreppet övertoner är högre i frekvens än det grundläggande. Vad vi kallar fyrkantsvågens frekvens är antalet övergångar den gör per tidsenhet. Men gå tillbaka till dessa derivat - förändringshastigheterna som signalen gör är enorma jämfört med förändringshastigheterna i en sinusformat vid samma frekvens. Här är där vi stöter på de högre komponentfrekvenserna: de höga förändringshastigheterna har attributen för sinusvågor med högre frekvens . De höga frekvenserna antyds av de höga förändringshastigheterna i den fyrkantiga (eller andra icke-sinusformade) signalen.

Den snabbt stigande kanten är inte typisk för en sinusform vid frekvensen f utan för en mycket högre frekvens sinusformad. Det fysiska systemet följer det så bra som möjligt men är hastighetsbegränsat och svarar mycket mer på de lägre frekvenskomponenterna än på de högre. Så vi saktar människor ser större amplitud, lägre frekvensrespons och kallar det f !

I praktiken är orsaken till att övertoner "uppträder" att linjära filtreringskretsar (liksom många icke-linjära filtreringskretsar) som är utformade för att detektera vissa frekvenser kommer att uppfatta vissa vågformer med lägre frekvens som de frekvenser de är intresserad av. För att förstå varför, tänk dig en stor fjäder med en mycket tung vikt som är fäst vid ett handtag via ganska lös fjäder. Att dra i handtaget flyttar inte den tunga vikten direkt så mycket, men den stora fjädern och vikten kommer att ha en viss resonansfrekvens, och om man flyttar handtaget fram och tillbaka med den frekvensen kan man lägga energi till den stora vikten och fjädern , ökar svängningens amplitud tills den är mycket större än vad som skulle kunna produceras "direkt" genom att dra i den lösa fjädern.

Det mest effektiva sättet att överföra energi till den stora fjädern är att dra i ett jämnt mönster som motsvarar till en sinusvåg - samma rörelsemönster som den stora fjädern. Andra rörelsemönster fungerar dock. Om man flyttar handtaget i andra mönster kommer en del av den energi som läggs i fjäderviktenheten under delar av cykeln att tas ut under andra. Antag som ett enkelt exempel att man helt enkelt fastnar i handtaget till de yttersta ändarna av färd med en hastighet som motsvarar resonansfrekvensen (motsvarande en fyrkantig våg). Att flytta handtaget från den ena änden till den andra precis när vikten når slutet av färdet kommer att kräva mycket mer arbete än vad som väntar på att vikten ska flyttas tillbaka lite först, men om man inte flyttar handtaget i det ögonblicket, fjädern på handtaget kommer att slåss mot vikten försök att återvända till centrum. Ändå skulle det ändå fungera tydligt att flytta handtaget från en extrem position till en annan.

Antag att det tar en sekund att svänga från vänster till höger och ytterligare en sekund att svänga tillbaka. Tänk nu på vad som händer om man flyttar handtaget från en extrem rörelse till det andra har gjort tidigare, men dröjer kvar i tre sekunder på varje sida istället för en sekund. Varje gång man förflyttar handtaget från det ena till det andra kommer vikten och fjädern att ha väsentligen samma position och hastighet som de hade två sekunder tidigare. Följaktligen kommer de att ha ungefär lika mycket energi till sig som de skulle ha haft två sekunder tidigare. Å andra sidan kommer sådana tillskott av energi bara att ske en tredjedel så ofta som de skulle ha gjort när "långvarig tid" bara var en sekund. Att flytta handtaget fram och tillbaka vid 1 / 6Hz kommer således att lägga en tredjedel så mycket energi per minut (effekt) till vikten som att flytta det fram och tillbaka vid 1 / 2Hz. En liknande sak händer om man flyttar handtaget fram och tillbaka vid 1 / 10Hz, men eftersom rörelserna blir 1/5 så ofta som vid 1 / 2Hz blir effekten 1/5.

Nu antar att istället för att ha kvarvarandetiden en udda numrerad multipel, gör man den till en jämn nummerad multipel (t.ex. två sekunder). I detta scenario kommer vikten och fjäderns position för varje vänster-till-höger-rörelse att vara densamma som dess position vid nästa höger-till-vänster-rörelse. Följaktligen, om handtaget tillför någon energi till fjädern i den förra, kommer denna energi i huvudsak att avbrytas av den senare. Följaktligen kommer våren inte att röra sig.

Om man istället för att göra extrema rörelser med handtaget, flyttar man det smidigare, så vid lägre frekvenser av handtagets rörelse är det lämpligt att det kommer fler gånger när man kämpar rörelsen för vikt / fjäderkombinationen. Om man flyttar handtaget i ett sinus-vågmönster, men med en frekvens som väsentligen skiljer sig från systemets resonansfrekvens, kommer den energi som man överför till systemet när man trycker på "rätt" väg att balanseras ganska bra av den energi som tas ur systemet och trycker på "fel" sätt. Andra rörelsemönster som inte är så extrema som fyrkantvågen kommer, åtminstone vissa frekvenser, att överföra mer energi till systemet än vad som tas ut.

en ännu enklare analogi är att föreställa sig en studsmatta.

Elektrificering av en ledare är analog med att sträcka studsmatta-membranet, vilket gör att "sträcker" energifält som är kopplade till den ledningen.

gå mitt i studsmattan, sträck dig ner och ta tag i studsmattans golv. stå nu upp och dra / sträck upp den när du går, så det är en topp ungefär midjans höjd.

Detta har naturligtvis effekten att lagra lite energi i membranet.

nu, om du bara släpper det, flyter det inte bara försiktigt ner och slutar röra sig. det kommer att snäppa ner snabbt och sedan VIBRERA ... oscillerar fram och tillbaka ett gäng fler gånger "på egen hand" ... när det går ner på sin lagrade energi.

om du istället gradvis sänker tillbaka den på plats ... kan den inte knäppa våldsamt var som helst och så får ingenting att / vibrera "på egen hand". det enda som vibrerar är att du flyttar det.

alla frekvenser (av vilken vågform som helst) har matematiska övertoner, vågformer med plötsliga potentiella förändringar ger en lättare möjlighet för dessa övertoner att uttryckas som verkliga världssvängningar.

Bara ett komplement till den här frågan,

Är dessa övertoner irrelevanta i saker som dataöverföring (hög = 1, låg = 0) och spelar bara roll i situationer som ljud eller RF?

att jag tror att ingen sa: Det är inte irrelevant. Vanligtvis är vi intresserade av att sända pulser i digitala kretsar så i de flesta fall tar vi inte hänsyn till denna vågfenomenologi. Detta beror på att även om fyrkantvågen har sina övertoner (inte oändligt antal övertoner i verkliga världen) så att det tar lite tid att stiga / falla, är din kretsdesign vanligtvis "medveten" om det. Detta är en av de största fördelarna med digital elektronik / digital kommunikation: från en given punkt (spänning) upp, tolkas signalen som 1 och från en given punkt och ner är den 0. I de flesta fall spelar det ingen roll det exakta formatet av fyrkantvågen eftersom den uppfyller vissa tidsspecifikationer.

Men notera att om din fyrkantiga signalfrekvens stiger upp till en punkt där våglängden är ungefär i storleksordningen av dess överföringsledning (kan vara en ledande spår av ett kretskort), då kan du ta hänsyn till denna vågfenomenologi. Du har fortfarande en krets i handen men vissa vågfenomen kan uppstå. Så beroende på din "linje" -impedans kan vissa frekvenser ha olika utbredningshastighet för andra frekvenser. Eftersom fyrkantvågen består av många övertoner (eller helst oändligheten) kommer du förmodligen att ha en förvrängd fyrkantvåg i slutet av din överföringsledning eller ledande spår (eftersom varje överton övergår med olika hastighet).

Ett bra exempel där detta kan hända är när vi använder USB-dataöverföring i en krets. Observera att datahastigheten är mycket hög (högfrekventa fyrkantiga vågor) så du måste ta hänsyn till impedansen för din överföringsledning. Annars har du förmodligen problem i kommunikationen.

Kort sagt, allt spelar roll och allt fungerar tillsammans men det är upp till dig att analysera om dessa saker är viktiga i ditt projekt / analys eller inte.